9. Конечные автоматы
Конечный автомат (так же встречается машина с конечным набором состояний, англ. finite state machine, fsm) — это концепция описания поведения последовательной логики с целью абстрагирования от структуры последовательных схем.
Термин исходит из теории автоматов (раздела дискретной математики), в которой существует понятие абстрактный автомат (abstract machine) — это теоретическая модель функционирования компьютерных систем. По аналогии с математическими функциями, абстрактный автомат также имеет набор входов, выходов, состояний и правил взаимодействия между входами, выходами и переходами:
| Математическая функция \( y=f(x) \) | Абстрактный автомат |
|---|---|
| Аргументы (\( x \)) | множество входов |
| функция (\( y \)) | множество выходов |
| уравнение зависимости (\( f(x) \)) | модель поведения |
В литературе часто можно встретить следующее обозначение автомата:
\( A=(X,Y,S,F_y,F_s) \),
где:
\( X \) — множество входных сигналов автомата,
\( Y \) — множество выходных сигналов автомата,
\( S\) — множество состояний автомата,
\( F_y \) — функции, описывающие значения выходов,
\( F_s \) — функции, описывающие условия переходов между состояниями.
Когда множества \( X \), \( Y \) и\( S \) являются конечными, такие автоматы называют конечным автоматом (КА, англ. finite state machine, fsm). Здесь и далее мы будем оперировать этим термином.
Функции описания переходов реализуют так называемое бинарное отношение между множеством входных сигналов автомата и множеством состояний. Такое отношение определяет в какое состояние автомат перейдет в следующий (t+1) момент времени:
\( s(t+1) = f_s(x(t),s(t)) \),
где \( s\) — это состояние из множества \( S\).
Функции описания значений выходов характеризуют состояние выходных сигналов относительно множества входов и текущего состояния КА:
\( y(t) = f_y(x(t),s(t)) \),
где \( y\) — это выход из множества \( Y\).
Можно заметить, что описание переходов КА напоминает поведение последовательной логики, а описание выходов схемы — комбинационной логики. Именно эта связь и используется при абстракции описания последовательных схем при помощи КА. Исторически сам автомат представляется в виде черной коробки, на входах которой в каждый момент времени t имеется некоторое значение. Это значение преобразуется через функции переходов в значение следующего состояния КА и сигналов для выходных портов Y, определяемых также через функции.
Рассмотрим способы составления и представления КА на примере следующей задачи:
На четырехбитный вход схемы последовательно вводят числа для ввода пароля 4х-значного пароля. При правильной последовательности чисел необходимо разблокировать дверь и зажечь зеленый светодиод, после чего выключить светодиод и закрыть дверь. При неправильной последовательности зажечь красный светодиод.
Назовем автомат, который будем описывать далее, \( FSM \). Примем, что
В множество входов \( X \) конечного автомата, описывающего такое поведение, входит только четырехбитных вход чисел. Обозначим его dataIn.
Множество выходов \( Y \) — это зеленый светодиод (ledg), красный светодиод (ledr), и сигнал открытия двери (doorOpen).
Множество состояний автомата \( S \) перечислить сложнее. Для начала точно известно, что есть начальное состояние (\(\(S_0\)), в котором принимается первое значение пароля. Так же можно сделать вывод, что должно быть состояние открытия двери ( \( S_{open}\)) и состояние ошибки ( \( S_{err}\)). В состояние \( S_{open}\) можно попасть только если все четыре значения введены верно, в состояние ошибки нужно попасть если хотя бы одно из значений было введено неверно, но только после ввода всей последовательности.
Определив часть состояний уже можно описать функции для выходов уравнениями булевой алгебры:
\( ledg = (FSM == S_{open}) \)— зеленый светодиод загорится только когда КА будет в состоянии открытия двери, во всех других случаях будет выключен;
\( doorOpen = (FSM == S_{open}) \) — дверь откроется только когда КА будет в состоянии открытия двери;
\( ledr = (FSM = S_{err}) \) — красный светодиод загорится только когда КА будет в состоянии ошибки.
При составлении конечных автоматов существует несколько способов описания, одним из удобных и наглядных способов представления считается граф переходов. Пример такого графа для перечисленных выше состояний можно увидеть ниже:
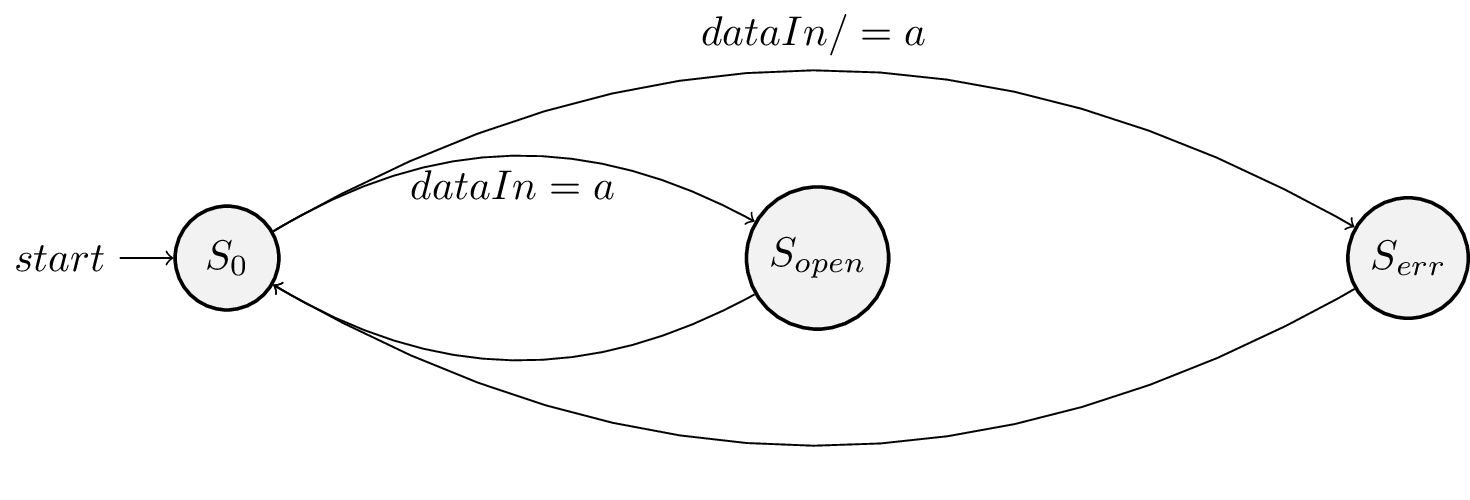
Приведенный на рисунке граф можно интерпретировать следующим образом: "конечный автомат начинается в \( S_0\), если на входе dataIn символ a — КА переходит в состояние \( S_{open}\), из которого безусловно возвращается обратно в \( S_0\). Если на входе был любой другой символ, КА переходит в \( S_{err}\), из которого безусловно возвращается обратно в \( S_0\)".
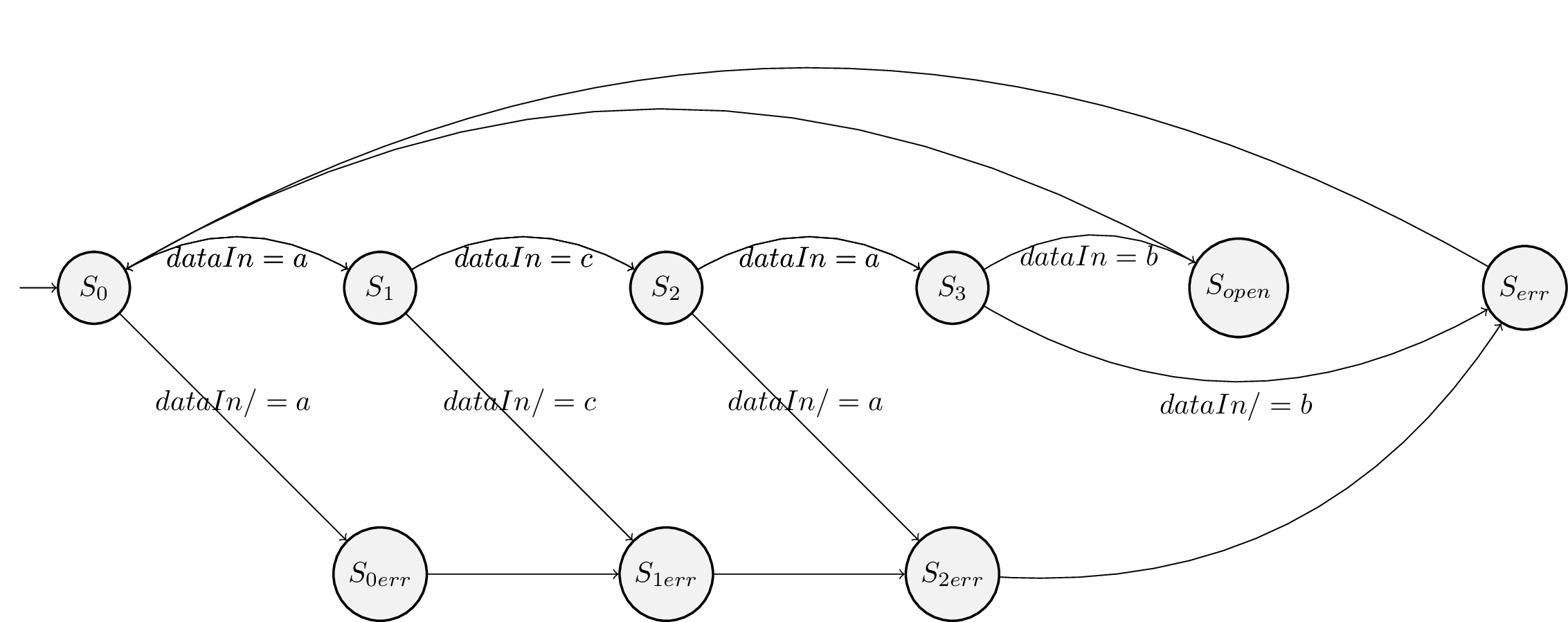
Исходя из этого описания можно понять, что полный функционал задачи не реализован: в данном графе обрабатывается только первый символ пароля, после которого дверь либо открыта либо нет. Для обработки следующих символов можно добавить дополнительные состояния проверки следующих символов, а также состояний ожидания ввода оставшихся символов когда первый уже оказался неверным.